Calculation for Electric Field Vectors
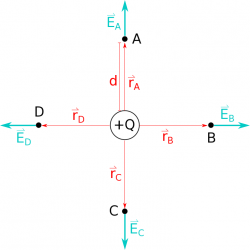 We can follow a very similar process for Points B-D as we did to calculate the electric field for Point A. For Point B, we start with:
$$\vec{E_B} = \frac{1}{4 \pi\epsilon_0}\frac{Q}{r_B^2} \hat{r_B}$$
Now $\vec{r_B}$ has the same length as $\vec{r_A}$ but points only in the +x direction
$$\vec{r_B}=\langle d,0,0 \rangle$$
So the magnitude and unit vector are given by:
$$r_B=|\vec{r_B}|=\sqrt{r_{Bx}^2+r_{By}^2+r_{Bz}^2}=\sqrt{d^2+0^2+0^2}$$
$$r_B = d$$
$$\hat{r_B}=\frac{\vec{r_B}}{r_B}=\frac{\langle d,0,0 \rangle}{d}=\langle 1,0,0 \rangle$$
$$\hat{r_B}=\langle 1,0,0 \rangle = \hat{x}$$
So at Point B, we find that the electric field points only in the +x direction and is given by:
$$\vec{E_B} = \frac{1}{4 \pi\epsilon_0}\frac{Q}{d^2} \hat{x}$$
The magnitude of the electric field at Point B is the same as the electric field at Point A ($|\vec{E_A}|=|\vec{E_B}|=\frac{1}{4 \pi\epsilon_0}\frac{Q}{r_B^2}$) so we would draw the electric field vector at Point B with the same length as the vector at Point A, but pointing in the +x-direction.
We can follow a very similar process for Points B-D as we did to calculate the electric field for Point A. For Point B, we start with:
$$\vec{E_B} = \frac{1}{4 \pi\epsilon_0}\frac{Q}{r_B^2} \hat{r_B}$$
Now $\vec{r_B}$ has the same length as $\vec{r_A}$ but points only in the +x direction
$$\vec{r_B}=\langle d,0,0 \rangle$$
So the magnitude and unit vector are given by:
$$r_B=|\vec{r_B}|=\sqrt{r_{Bx}^2+r_{By}^2+r_{Bz}^2}=\sqrt{d^2+0^2+0^2}$$
$$r_B = d$$
$$\hat{r_B}=\frac{\vec{r_B}}{r_B}=\frac{\langle d,0,0 \rangle}{d}=\langle 1,0,0 \rangle$$
$$\hat{r_B}=\langle 1,0,0 \rangle = \hat{x}$$
So at Point B, we find that the electric field points only in the +x direction and is given by:
$$\vec{E_B} = \frac{1}{4 \pi\epsilon_0}\frac{Q}{d^2} \hat{x}$$
The magnitude of the electric field at Point B is the same as the electric field at Point A ($|\vec{E_A}|=|\vec{E_B}|=\frac{1}{4 \pi\epsilon_0}\frac{Q}{r_B^2}$) so we would draw the electric field vector at Point B with the same length as the vector at Point A, but pointing in the +x-direction.
By now, you may have noticed a pattern - for any point that is a distance d away from the point charge, the magnitude of the electric field will be same. Which means for Points C and D, we really only need to determine the direction of the electric field. For Point C, the separation vector will point down (from the charge to Point C), so we write $\vec{r_C}$ as: $$\vec{r_C} = \langle 0,-d,0 \rangle$$ Then the magnitude and unit vector are found in exactly the same way: $$r_C=|\vec{r_C}|=\sqrt{r_{Cx}^2+r_{Cy}^2+r_{Cz}^2}=\sqrt{0^2+(-d)^2+0^2}=d$$ $$\hat{r_C}=\frac{\vec{r_C}}{r_C}=\frac{\langle 0,-d,0 \rangle}{d}=\langle 0,-1,0 \rangle$$ $$\hat{r_C}=\langle 0,-1,0 \rangle = -\hat{y}$$
So the electric field at Point C is given by $$\vec{E_C} = - \frac{1}{4 \pi\epsilon_0}\frac{Q}{d^2} \hat{y}$$ and would be drawn with the same length but pointing downwards at Point C. Note that there is now a negative sign in the electric field equation - this is because at Point C the electric field points downward, not because the charge is now suddenly negative.
Following the same patterns, we can say that the electric field at Point D will be (though you can do the math on your own if you would like): $$\vec{E_D} = - \frac{1}{4 \pi\epsilon_0}\frac{Q}{d^2} \hat{x}$$ which we would draw with the same magnitude but pointing in the -x direction.